扩展欧几里德算法的原理与实现

欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。而扩展欧几里德算法是用来在已知a, b求解一组x，y使得ax+by = gcd(a, b) =d(解一定存在，根据数论中的相关定理)。扩展欧几里德常用在求解模线性方程及方程组中。

在介绍扩展欧几里德算法之前,先来看一下欧几里德算法.

欧几里德算法

欧几里德算法又称辗转相除法,用于计算两个整数a,b的最大公约数。C++语言实现如下:

而扩展欧几里德算法是给两个整数 a,b 必然存在 一对整数 x,y 使得 ax + by = gcd(a,b) .(又叫贝祖定理).

由朴素的欧几里德算法可以得道, gcd(a,b) == gcd(b,a%b); 那么就有了如下的推断:

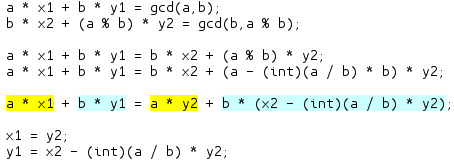
在上式中.两个等式右边满足欧几里德算法,所以有了a*x1+b*y1=b*x2+(a%b)*y2; 经过化简,得到x1,y1与x2,y2的关系.(最后两个等式)

扩展欧几里德算法

下面来看扩展欧几里德算法,以这个题目为例:

已知等式 47x + 30y = 1;求x,y的整数解.

设扩展欧几里德算法为gcdEx(a,b,x,y); 其中a,b为已知,x,y为所求.那么gcdEx(a,b,x,y)函数就有如下的计算过程:

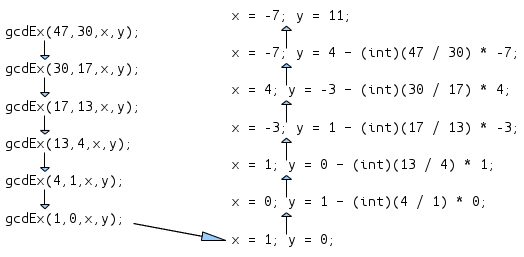
左边,是利用朴素欧几里德算法相除得到一系列中间值,直到b=0.当b=0时,开始倒回去,令x=1;y=0;往上一步的x,y看作x1,y1.下面'旧'的x,y看作x2,y2.利用朴素欧几里德算法推导出的结论,x1=y2,y1=x2-(a/b)*y2;其中,a,b就是当前gcdEx中的a,b.当这样递归回去到了第一个调用点时,所得到的x,y就是结果,即x=-7,y=11;

当然,此题目刚好满足ax+by=gcd(a,b); 其实,对于任意的ax+by=c;若c为gcd(a,b)的整数倍,即存在整数解.

C++ 语言实现扩展欧几里德算法