有n个格子,从左到右放成一排,编号为1-n。共有m次操作,有3种操作类型:1.修改一个格子的权值,2.求连续一段格子权值和,3.求连续一段格子的最大值。对于每个2、3操作输出你所求出的结果。
输入格式
第一行2个整数n,m。
接下来一行n个整数表示n个格子的初始权值。
接下来m行,每行3个整数p,x,y,p表示操作类型,p=1时表示修改格子x的权值为y,p=2时表示求区间[x,y]内格子权值和,p=3时表示求区间[x,y]内格子最大的权值。
输出格式
有若干行,行数等于p=2或3的操作总数。
每行1个整数,对应了每个p=2或3操作的结果。
样例输入
4 3
1 2 3 4
2 1 3
1 4 3
3 1 4
样例输出
6
3
数据规模与约定
对于20%的数据n <= 100,m <= 200。
对于50%的数据n <= 5000,m <= 5000。
对于100%的数据1 <= n <= 100000,m <= 100000,0 <= 格子权值 <= 10000。
解题思路
难点应该在修改数据这里,这里对总值的影响还比较好解决,对最大值的影响就比较难了,因为不知道当前修改的是不是最大值,如果是最大值,又不知道次大值是多少.
我的解决方案是,当修改数据时,重置它的所有父节点的最大值.然后再查询一下这个值,在查询时恢复最大值.
另外,修改数据时返回一个变动差,表示与上次数据的差距,把它的所有父节点加上这个变动差就可以解决修改时造成的和的变化.
测试用例和代码
测试用例
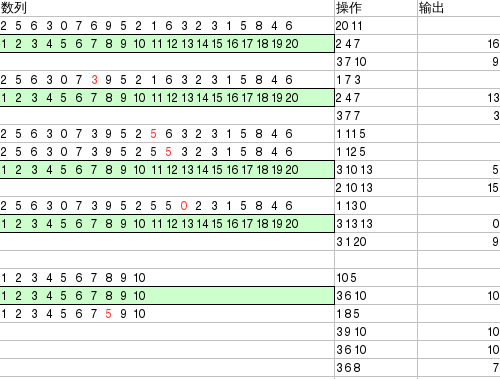


 在没有特别指明时以
在没有特别指明时以